针孔和鱼眼模型下的摄像机几何
本文描述单摄像机下射影几何关系,推导针孔相机下空间中的3维坐标到相机成像平面坐标和像素坐标的转化过程,并计算鱼眼相机和针孔摄像相机在坐标之间的相互关系,并列举常见的畸变函数
针孔模型
点到平面的投影
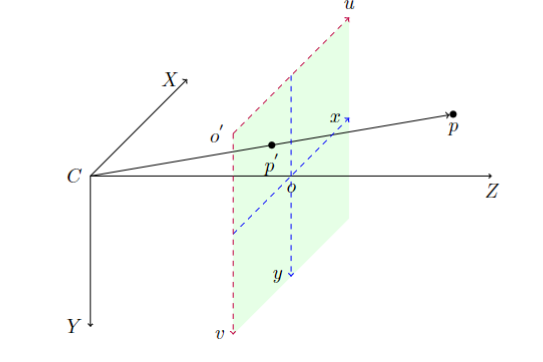
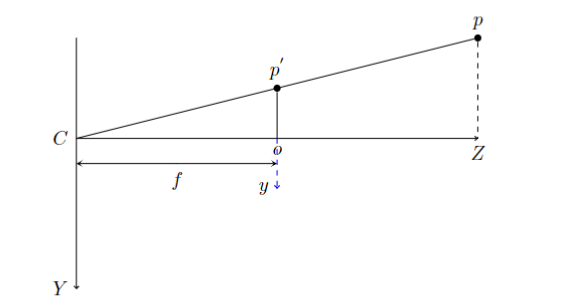
我们考虑空间点到一张平面上的中心投影. 投影中心位于一个欧氏坐标系的原点, 而平面$z=f$被称为图像平面.在针孔摄像机模型下, 间坐标为$P=(X,Y,Z)$ 的点 被映射到图像平面上的点,该点是连接点投影中心的直线与图像平面的交点 $P^{'}$ 如下图
使用相似三角形可以轻松的计算$P^{'}$在图像平面坐标系下$0-x-y$的,如图,所以相机世界坐标系到图像平面坐标系的坐标转换可以表示如下:
\[\begin{eqnarray*} f: R^3 &\rightarrow& R^2 \\ \left(\begin{matrix} x \\ y\\ z \end{matrix}\right) &\mapsto& \left(\begin{matrix} f \frac{x}{z}\\ f \frac{y}{z} \end{matrix}\right) =\frac{1}{z} \left[\begin{matrix} f&0&0 \\ 0&f&0 \\ \end{matrix} \right] \left(\begin{matrix} x \\ y\\ z \end{matrix}\right) \end{eqnarray*}\]也可以使用其次坐标系表示投影:
\[\begin{eqnarray*} f: R^3 &\rightarrow& R^3 \\ \left(\begin{matrix} x \\ y\\ z \end{matrix}\right) &\mapsto& \left(\begin{matrix} fx\\ fy \\1 \end{matrix}\right)= \frac{1}{z} \left[\begin{matrix} f&0&0 \\ 0&f&0 \\ 0&0&1 \\ \end{matrix}\right]\left(\begin{matrix} x \\ y\\ 1 \end{matrix}\right) \end{eqnarray*}\]像素坐标计算
接下来我们计算点$P^{'}$在像素坐标系$o^{'}-u-v$下的像素坐标,首先考虑到$0-x-y$与$o^{'}-u-v$的坐标系得单位刻度不同,我们假设坐标系$o^{'}-u-v$相对$0-x-y$缩放了$\left(\alpha,\beta\right)$,如果$0-x-y$得单位刻度为米,则$\alpha$和$\beta$得单位为:像素/米。其次坐标系$0-x-y$沿着向量$\overrightarrow{oo^{'} }=\left(c_x,c_y\right)$位移到坐标系$o^{'}-u-v$,所以从坐标系$0-x-y$到像素坐标系$o^{'}-u-v$得完整变换为
\[\begin{eqnarray*} h: R^2 &\rightarrow& R^2 \\ \left(\begin{matrix} x \\ y \end{matrix}\right) &\mapsto& \left(\begin{matrix} u \\ v \end{matrix}\right)=\left(\begin{matrix} \alpha \cdot x\\ \beta \cdot y \end{matrix}\right)+\left(\begin{matrix} c_x \\c_y \end{matrix} \right) \end{eqnarray*}\]用其次坐标表示如下:
\[\begin{eqnarray*} h: R^2 &\rightarrow& R^2 \\ \left(\begin{matrix} x \\ y \\ 1 \end{matrix}\right) &\mapsto& \left(\begin{matrix} u \\ v \\1 \end{matrix}\right)=\left(\begin{matrix} \alpha & 0& c_x \\ 0&\beta & c_y \\ 0&0&1 \end{matrix}\right)\left(\begin{matrix} x \\y \\1 \end{matrix} \right) \end{eqnarray*}\]将$f$和$h$复合可以得到针孔模型相机坐标系到像素坐标系得完整变化,结构如下
\[\begin{eqnarray*} h \circ f: R^3 &\rightarrow& R^2 \\ \left(\begin{matrix} x \\ y \\ z \end{matrix}\right) &\mapsto& \left(\begin{matrix} u \\ v \\1 \end{matrix}\right)=\frac{1}{z} \left(\begin{matrix} \alpha \cdot f& 0& c_x \\ 0&\beta \cdot f & c_y \\ 0&0&1 \end{matrix}\right)\left(\begin{matrix} x \\y \\z \end{matrix} \right) \end{eqnarray*}\]令
\[\begin{eqnarray*} K=\left(\begin{matrix} \alpha \cdot f& 0& c_x \\ 0&\beta \cdot f & c_y \\ 0&0&1 \end{matrix}\right)\circeq \left(\begin{matrix} f_x& 0& c_x \\ 0&f_y & c_y \\ 0&0&1 \end{matrix}\right) \end{eqnarray*}\]$K$即为相机得内参矩阵。
鱼眼畸变
在使用中我们常常会在摄像机得前方加上透镜来获得更好得视角范围,称为鱼眼相机模型。由于增加透镜会引起图形畸变.下面我们推到针孔模型到鱼眼模型(加畸变)和鱼眼模型到针孔模型(取畸变)的数学过程。
针孔摄像头到鱼眼镜头
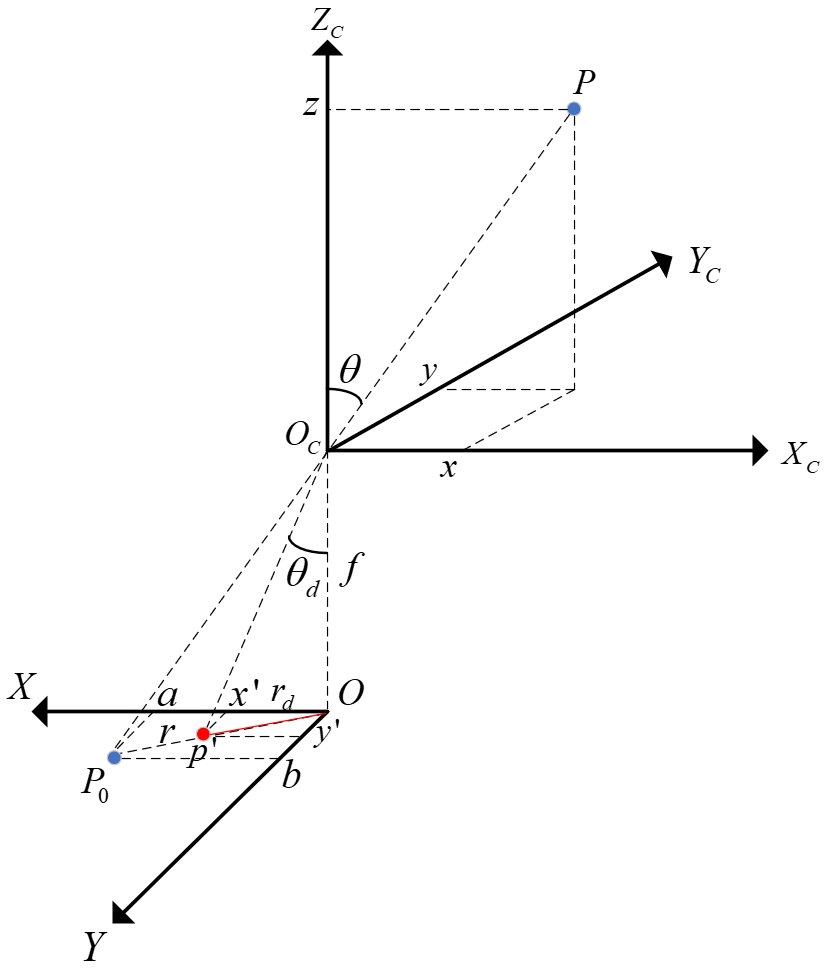
如图,坐标系$O_c-X_cY_cZ_c$是相机的世界坐标系,坐标系$O-XY$是相机成像平面坐标系 点$P$为点在空间的位置,点$P_0$为针孔模型下$P$在归一化坐标系的坐标,$P^{'}$为鱼眼模型下 $P$在的归一化坐标,$\theta$为$P$与$Z_c$的夹角称为视角,$r_d$为$P^{'}$的模长称为像高,$f$ 为焦距,后续统一默认为$1$.现在推理$P$的鱼眼像素坐标计算过程。
假设$P_0$的坐标为$(x_0,y_0)$,$P^{'}$的坐标为$(X^{'},Y^{'})$,由图可得
\[\begin{eqnarray*} r&&=\sqrt{(x_0^2+y_0^2)}\\ \theta&&=\arctan(r/f)=\arctan(r) \end{eqnarray*}\]假设相角$\theta$和视高$r_d$,满足函数$r_d=f_{\theta}(\theta)$。因为三角形$\bigtriangleup OP_0X_0$和 $\bigtriangleup OP^{'}X^{'}$相似,可得\
\[\frac{x_0}{x^{'}}=\frac{r}{r_d}\]同理
\[\frac{y_0}{y^{'}}=\frac{r}{r_d}\]最好假设摄像机的内参分别为$f_x$ $f_y$ $c_x$ $c_y$,则$P^{'}$的像素坐标$(u,v)$为
\[\begin{eqnarray*} u=f_xx^{'}+c_x \\ v=f_yy^{'}+c_y \end{eqnarray*}\]鱼眼镜头到针孔摄像头
如图,坐标系$O_c-X_cY_cZ_c$是相机的世界坐标系,坐标系$O-XY$是相机归一化坐标系 点$P$为点在空间的位置,点$P_0$为针孔模型下$P$在归一化坐标系的坐标,$P^{'}$为鱼眼模型下 $P$在的归一化坐标,$\theta$为$P$y与$Z_c$的夹角称为视角,$r_d$为$P^{'}$的模长称为像高,$f$ 为焦距,后续统一默认为$1$.现在推理$P$的鱼眼像素坐标计算过程。
假设$P_0$的坐标为$(x_0,y_0)$,$P^{'}$的坐标为$(x^{'},y^{'})$,由图可得
\[\begin{eqnarray*} r_d=\sqrt{((x^{'})^2+(y^{'})^2)} \end{eqnarray*}\]假设相角$\theta$和视高$r_d$,满足函数$\theta=f_{r}(r_d)$。所以$r=tan(\theta)$ 因为三角形$\bigtriangleup OP_0X_0$和 $\bigtriangleup OP^{'}x^{'}$相似,可得
\[\frac{x_0}{x^{'}}=\frac{r}{r_d}\]同理
\[\frac{y_0}{x^{'}}=\frac{r}{r_d}\]最好假设摄像机的内参分别为$f_x$ $f_y$ $c_x$ $c_y$,则$P_0$的像素坐标$(u,v)$为
\[\begin{eqnarray*} u=f_xx_0+c_x \\ v=f_yy_0+c_y \end{eqnarray*}\]投影函数
| 透视投影 (perspective projection) | $r=f_{\theta}\tan(\theta)$ | 针孔相机模型 |
| 体视投影 (stereographic projection) | $r=2f_{\theta}\tan(\frac{\theta}{2})$ | 任何直线相交的角度,在变换后保持不变 |
| 等距投影 (equidistance projection) | $r=f_{\theta}\theta$ | 物体成像面上距离画面中心的距离与入射角成正比 |
| 等积投影 (equisolid angle projection) | $r=2f_{\theta}\sin(\frac{\theta}{2})$ | 在变换前后,物体所占的立体角大小不变 |
| 正交投影 (orthogonal projection) | $r=f_{\theta}\sin(\theta)$ | 投影畸变最大,而且最大视场角不能大于180° |