LK光流法的基本概念

本文描述光流的基本概念和光流不等式，最后简单介绍LK光流的求解原理

光流法

光流等式

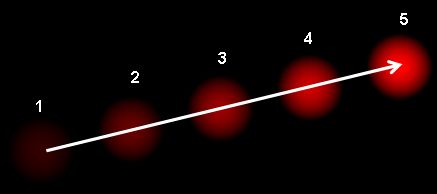
光流是由物体或相机的运动引起的图像物体在两个连续帧之间的明显运动模式。 它是 2D 矢量场，其中每个矢量都是一个位移矢量，显示点从第一帧到第二帧的移动。 如图\ref{pic1}（图片提供：维基百科关于光流的文章）。

考虑第一帧像素$I(x,y,t)$,在下一帧沿向量移动了$(dx,dy)$,两帧间隔$dt$,假设这些 像素在两帧之间像素灰度不变

\[I(x,y,t)=I(x+dx,y+dy,t+dt)\]

对等号右边进行一阶泰勒展开，可得

\[dx*I_x+dy*I_y+dt*I_t=0\]

等式同时除以$dt$可得

\[\frac{dx}{dt}I_x+\frac{dy}{dt}I_y+I_t=0\]

令$u=\frac{dx}{dt}$和$v=\frac{dy}{dt}$ 可得光流等式

\[u*I_x+v*I_y+I_t=0\]

LK光流

光流不等式是一个二元一次方式，为了能求解出$u$和$v$,假设像素的邻域和像素同运动, LK光流假设$3\times 3$的方块内像素同运动.这样我们就可以得到九个光流等式：

\[\begin{eqnarray} \left[\begin{matrix} I_{1x}&I_{1y} \\ \vdots& \vdots \\ I_{9x}&I_{9y} \end{matrix}\right]\left(\begin{matrix} u\\v \end{matrix}\right)=-\left[\begin{matrix} I_{1t} \\ \vdots \\ I_{9t} \end{matrix} \right] \end{eqnarray}\]

通过求解上式的最小二乘解就可以的到$\left(u,v\right)$的最优价。